Вычисления работы электрического поля по перемещению заряда
Мы уже указывали на сходство законов взаимодействия электрически заряженных тел (закон Кулона) и массивных тел (закон всемирного тяготения). В обоих случаях
![]()
Соответственно и последствия из законов должны быть похожими.
В курсе механики мы выяснили, что сила всемирного тяготения является консервативной силой, поскольку ее работа по перемещению тела массой m в пространстве не зависит от траектории движения тела, а определяется только его начальным и конечным положениями. Работа по перемещению тела по замкнутой траектории равна нулю. Работа силы земного притяжения (у поверхности Земли) A = mg (h1 — h2 ) (обозначение см. рис. ниже); во всемирном масштабе работа гравитационной силы
![]()
Напоминаем, что силовое поле, в котором работа не зависит от формы траектории, называют потенциальным.
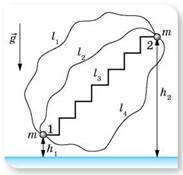
В каждой точке поля тело имеет определенную потенциальную энергию относительно выбранного нулевого уровня. Значение потенциальной энергии тела в данной точке пространства определяется работой поля по перемещению тела от этой точки на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела A = — (Еп2 — Эп1 ).
Эти выводы получены из закона всемирного тяготения Ньютона, подобные выводы должны быть получены и для электростатических сил, действующих в электрическом поле.
Рассмотрим движение точечного заряда в однородном электрическом поле. Пусть однородное поле создают большие металлические пластины, имеющие заряды противоположных знаков. Это поле действует на точечный тело постоянной силой
![]()
подобно тому, как поле тяготения действует с постоянной силой
![]()
на тело вблизи поверхности Земли.
Пусть пластины размещены горизонтально. Вычислим работу, которую выполняет электростатическое поле, перемещая положительный заряд q с точки 1, расположенной на расстоянии d1 от отрицательно заряженной пластины, в точку 2, удаленную на расстояние d2 , по прямолинейной траектории (а).
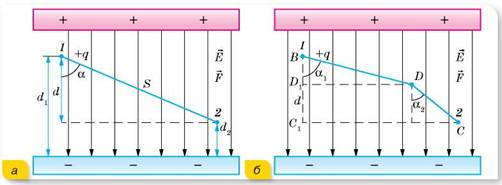
Как известно из курса механики, работа по перемещению тела определяется формулой A = Fscosα, где α — угол между векторами силы и перемещения.
Согласно электрическое поле на участке 1-2 выполняет работу A = Fd, где d = s cos α. С учетом того, что F = qE, получаем A = qEd = qE (d1 — d2 ). Эта работа не зависит от формы траектории, подобно тому, как не зависит от формы траектории работа силы тяжести. Докажем это. Пусть теперь положительный заряд q перемещается с точки 1 в точку 2 на ломаном ВDС (б). Тогда поле выполняет работу A = qE (BD cos α1 + DC cos α2 ) = qE (BD1+ D1 C1 ) = qEd.
К такому же выводу мы придем для любого вида траектории движения точечного заряда, ведь любую кривую можно заменить перемещением по ломаной траектории с достаточно малыми ступенями:
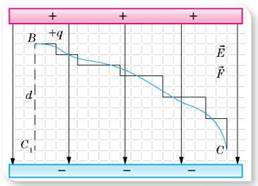
Мы доказали, что в однородном электрическом поле работа электростатических сил не зависит от формы траектории. Итак, работа по перемещению заряда по замкнутой траектории равна нулю.
Можно доказать, что этот вывод подтверждается и для неоднородных полей, например, для поля точечного заряда. В этом случае работу по перемещению положительного заряда q0 с точки 1, которая находится на расстоянии r1 от заряда q, что создает поле, в точку 2, которая находится на расстоянии r2 , определяют по формуле
![]()
независимо от формы траектории.
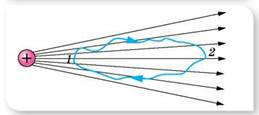
Итак, электростатические силы взаимодействия между неподвижными точечными зарядами являются консервативными. А поле консервативных сил потенциальным. Согласно этому электрическое поле, так же, как и гравитационное поле, — потенциальное. И работа сил электрического поля может быть определена из-за изменения потенциальной энергии точечного заряда в этом поле.
Потенциальная энергия взаимодействия точечных зарядов
Подобно тому, как любое тело, которое взаимодействует с Землей по закону всемирного тяготения, на разных расстояниях от ее центра имеет различную потенциальную энергию, электрический заряд q на разном расстоянии от другого заряда q0 имеет различную потенциальную энергию — W. Если заряд q перемещается в электрическом поле из точки 1, где его потенциальная энергия была W1, в точку 2, где его энергия стала W2 , работа сил поля A = W1 — W2 = -(W2 — W1) = -ΔW. Как видно из формулы, A и ΔW имеют противоположные знаки. Это объясняется тем, что если заряд q перемещается под действием сил поля (т.е. работа поля А положительная), то его потенциальная энергия уменьшается, прирост энергии ΔW — отрицательный. Если же заряд перемещается против сил поля (А — отрицательная), то потенциальная энергия заряда увеличивается. (Такое же соотношение между потенциальной энергией и работой силы тяжести.)
Поскольку буквой Е сказывается напряженность электрического поля, то энергию в электродинамике принято обозначать буквой W.
Как известно, значение потенциальной энергии зависит от выбора нулевого уровня. В электростатике условились потенциальную энергию заряда, размещенного в точке, бесконечно удаленной от заряженного тела, создает поле, считать нулем, W∞ = 0. Тогда, в случае перемещения заряда q с точки 1 в бесконечность, работа поля A = W1 — W∞ = W1 . То есть потенциальная энергия заряда q, размещенного в какой-либо точке поля, численно равна работе, которую выполняют силы поля, перемещая этот заряд с указанной точки в бесконечность: W = qEd, где d — расстояние от источника поля до точки, в которой находится заряд q.
В электротехнике, в отличие от электростатики, под нулем часто принимают потенциальную энергию заряда, размещенного на Земле.
Если поле создано положительным зарядом, то значение потенциальной энергии другого положительного заряда, размещенного в некоторой точке этого поля, будет положительным, если же поле создано отрицательным зарядом, то значение потенциальной энергии положительного заряда — отрицательно. Для отрицательного заряда, размещенного в электрическом поле, все будет наоборот. Когда поле создано сразу несколькими зарядами, потенциальная энергия заряда q, размещенного в какой-либо точке такого поля, равна алгебраической сумме энергий, обусловленных полем каждого заряда в этой точке.
